

Motion Planning (MP) is a critical challenge in robotics, especially pertinent with the burgeoning interest in embodied artificial intelligence. Traditional MP methods often struggle with high-dimensional complexities. Recently neural motion planners, particularly physics-informed neural planners based on the Eikonal equation, have been proposed to overcome the curse of dimensionality. However, these methods perform poorly in complex scenarios with shaped robots due to multiple solutions inherent in the Eikonal equation. To address these issues, this paper presents PC-Planner, a novel physics-constrained self-supervised learning framework for robot motion planning with various shapes in complex environments. To this end, we propose several physical constraints, including monotonic and optimal constraints, to stabilize the training process of the neural network with the Eikonal equation. Additionally, we introduce a novel shape-aware distance field that considers the robot's shape for efficient collision checking and Ground Truth (GT) speed computation. This field reduces the computational intensity, and facilitates adaptive motion planning at test time. Experiments in diverse scenarios with different robots demonstrate the superiority of the proposed method in efficiency and robustness for robot motion planning, particularly in complex environments.
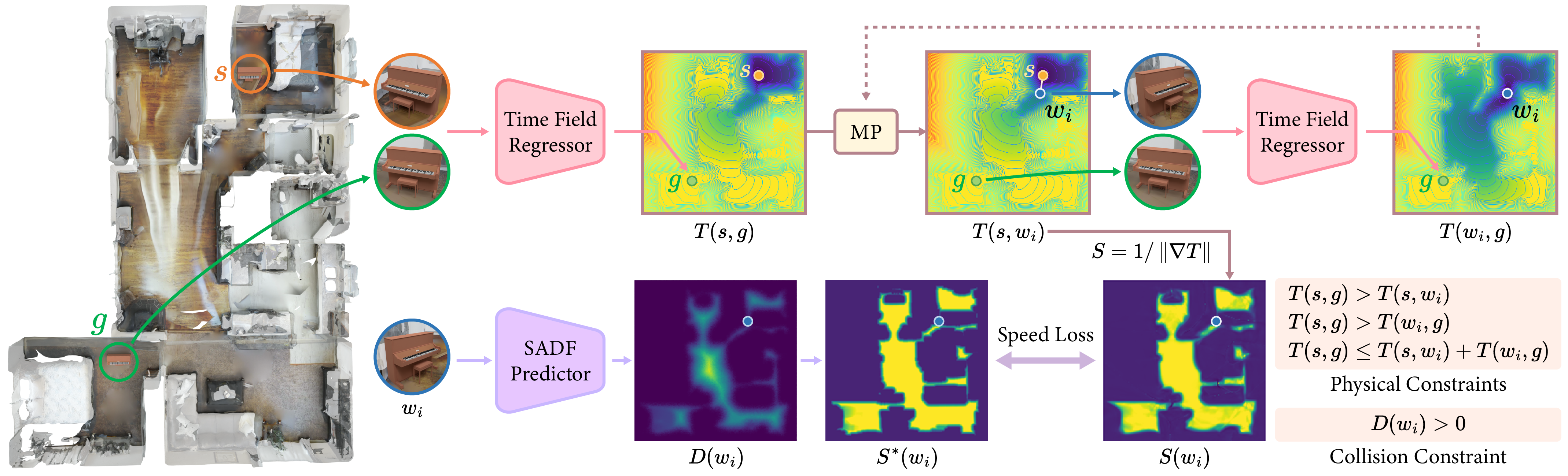
The PC-Planner integrates a physics-constrained self-supervised learning framework with a shape-aware distance field. The start configuration $\mathbf{s}$ and goal configuration $\mathbf{g}$ are utilized to predict the time $T(\mathbf{s}, \mathbf{g})$ through the time field regressor. The travel times $T(\mathbf{s}, \mathbf{g})$, $T(\mathbf{s}, \mathbf{w_i})$, and $T(\mathbf{w_i}, \mathbf{g})$ are employed to incorporate physical constraints during the training of the time field in a self-supervised manner to reduce local minima. It is essential that the waypoint $\mathbf{w_i}$ remains collision-free, which can be ensured by distance $D(\mathbf{w_i})$ predicted through SADF. Moreover, $D(\mathbf{w_i})$ can also be converted into the ground truth speed $S^*(\mathbf{w_i})$ of $\mathbf{w_i}$ to compute the speed loss with the predicted speed $S(\mathbf{w_i})$, which is determined using the time $T(\mathbf{s}, \mathbf{w_i})$ and Eikonal equation. During training, the motion planning (MP) iterates to derive the waypoint for physical constraint loss, while during testing, it iteratively computes waypoints to generate a path solution.
@article{shen2024pcplanner,
author = {Xujie Shen and Haocheng Peng and Zesong Yang and Juzhan Xu and Hujun Bao and Ruizhen Hu and Zhaopeng Cui},
title = {PC-Planner: Physics-Constrained Self-Supervised Learning for Robust Neural Motion Planning with Shape-Aware Distance Function},
year = {2024},
doi = {10.1145/3680528.3687651},
}